ما هي مساحة المثلث يعتبر المثلث من أشهر الأشكال الهندسية المعروفة والتي يستخدمها الكثير من الأشخاص، والمثلث هو شكل هندسي مغلق وقد يختلف من حيث مساحة أو طول الأضلاع التي يتكون منها فهناك المثلث متساوي الساقين أو المثلث متساوي الأضلاع، وهناك أيضا مختلف الأضلاع كما سوف نرى عبر موقع زيادة .
قانون مساحة المثلث
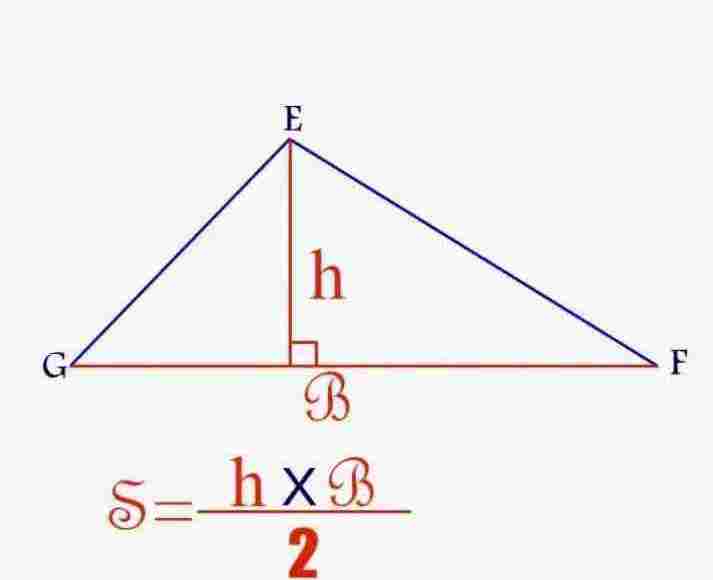
مساحة المثلث = ½ × القاعدة × الارتفاع
وهو قانون عام ينطبق على جميع أنواع المثلثات.
كيفية حساب مساحة المثلث
- ويمكن حساب مساحة المثلث أيضا من خلال قانون مختلف تماما عن القانون السابق، حيث لابد من توافر بعض المعطيات البسيطة أيضا لحساب هذه المساحة بشكل بسيط جدا وسهل، ولذلك يستخدم هذا الطريقة الصحيحة الكثير من الأشخاص أيضا.
- وبسهولة شديدة يمكن حساب مساحة المثلث إذا توافر طول ضلع واحد فقط من الأضلاع المختلفة الخاصة بالمثلث، بالإضافة إلى معرفة كلا من الزاويتين المجاورتين لهذا الضلع المعروف طوله بشكل صحيح وسليم.
- ويمكن حساب مساحة المثلث من خلال القانون الذي يعبر عن ذلك والذي يشمل ضرب كلا من طول الضلع المعروف في جا س في جا ص، وتعرف جا س بالزاوية الأولى التي تقع بجوار الضلع، وجا ص بالزاوية الثانية المجاورة للضلع أيضا.
- كما يمكن حساب مساحة المثلث بطريقة أخرى أكثر بساطة وسهولة من الطريقين السابقيتين، ولكن هذه الطريقة تتطلب بعض المعطيات الخاصة، حيث لابد من توافر الطول الصحيح لكل ضلع من أضلاع المثلث الثلاثة دون الاحتياج إلى زواياه.
- وينص القانون الخاص بحساب مساحة المثلث إذا توافر جميع أضلاعه على جمع كلا من أ بالإضافة إلى ب بالإضافة إلى ج ومن ثم نقوم بضرب هذا المجموع في رقم 2، ويعبر أ عن طول الضلع الأول، وب عن طول الضلع الثاني، وج عن الضلع الثالث.
القانون العام لحساب محيط المثلث
- يقوم الكثير من الأشخاص أو المهندسين والعلماء المتخصصين بحساب محيط المثلث من خلال الجمع بين جميع أضلاعه المختلفة، كما يمكن استخدام نفس الطريقة في الجمع لحساب المحيط الخاص بأي نوع من الأشكال الهندسية الأخرى.
- كما يوجد وحدة قياس معينة لقياس مساحة محيط المثلث وتعبر هذه الوحدة عن قياس المسافة الخطية أو الطول الواقع بين أحد الجوانب الموجودة في المثلث أو أي شكل هندسي آخر، ويرجع ذلك إلى التشابه بين محيط المثلث والأشكال الهندسية الأخرى.
- وينص القانون الأساسي والصحيح لحساب محيط المثلث الذي تتوافر جميع أضلاعه على الجمع بين أ وب وج، ويعبر أ عن طول الضلع الأول الموجود في المثلث، كما يعبر ب عن طول الضلع الثاني الموجود في المثلث، ويعبر ج عن طول الضلع الثالث.
أوضح هذا المقال الطريقة الصحيحة والمثالية لحساب مساحة المثلث سواء متساوي الأضلاع أو متساوي الساقين، كما أوضح أيضا بعض القوانين الخاصة بحساب محيط المثلث.